Shapes That Are Not Parallelograms

A parallelogram is a ii-dimensional geometrical shape whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length. The Sum of side by side angles of a parallelogram is equal to 180 degrees. In geometry, you must have learned nearly many 2D shapes and sizes such as circles, squares, rectangles, rhombus, etc. All of these shapes have a different ready of properties. Also, the area and perimeter formulas of these shapes vary from each other and are used to solve many problems. Permit us learn here the definition, formulas and properties of a parallelogram.

Parallelogram Definition

A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the contrary angles are equal in measure out. Also, the interior angles on the same side of the transversal are supplementary. The Sum of all the interior angles equals 360 degrees.

A iii-dimensional shape that has its faces in a parallelogram shape is called a parallelepiped. The area of the parallelogram depends on the base (one of its parallel sides) and its height (altitude drawn from top to bottom) of information technology. The perimeter of a parallelogram depends on the length of its 4 sides.

A square and a rectangle are 2 shapes which have like properties to a parallelogram.

Rhombus: If all the sides of a parallelogram are congruent or equal to each other, and then it is a rhombus.

If there is one parallel side and the other two sides are non-parallel, then information technology is a trapezium.

Encounter the figure beneath:

Parallelogram 1

In the figure above, you lot tin can see, ABCD is a parallelogram, where AB || CD and AD || BC.

Also, AB = CD and AD = BC

And,∠A = ∠C & ∠B = ∠D

Besides, ∠A & ∠D are supplementary angles because these interior angles lie on the same side of the transversal. In the aforementioned manner, ∠B & ∠C are supplementary angles.

Therefore,

∠A + ∠D = 180

∠B + ∠C = 180

Facts:

Number of sides = 4
Number of vertices = four
Mutually Parallel sides = 2 (in pair)
Area = Base of operations x Height
Perimeter = 2 (Sum of adjacent sides length)
Type of polygon = Quadrilateral

Shape of Parellelogram

A parallelogram is a two-dimensional shape. It has four sides, in which two pairs of sides are parallel. Also, the parallel sides are equal in length. If the length of the parallel sides is non equal in measurement, then the shape is not a parallelogram. Similarly, the opposite interior angles of a parallelogram should always be equal. Otherwise, it is not a parallelogram.

Special Parallelograms

Square and Rectangle: A square and a rectangle are two shapes which accept similar properties to a parallelogram. Both take their opposite sides equal and parallel to each other. Diagonals of both shapes bifurcate each other.

Rhomb: If all the sides of a parallelogram are coinciding or equal to each other, then information technology is a rhombus.

Rhomboid: A special case of a parallelogram that has its reverse sides parallel to each other but adjacent sides are of unequal lengths. Besides, the angles are equal to 90 degrees.

Trapezium: If at that place is one pair of side parallel and the other ii sides are non-parallel, and then it is a trapezium.

Angles of Parallelogram

A parallelogram is a flat 2d shape which has four angles. The opposite interior angles are equal. The angles on the same side of the transversal are supplementary, that means they add up to 180 degrees. Hence, the sum of the interior angles of a parallelogram is 360 degrees.

Properties of Parallelogram

If a quadrilateral has a pair of parallel opposite sides, information technology'due south a special polygon called Parallelogram. The backdrop of a parallelogram are as follows:

The opposite sides are parallel and equal
The opposite angles are equal
The consecutive or adjacent angles are supplementary
If any one of the angles is a right angle, then all the other angles volition be at right angle
The two diagonals bifurcate each other
Each diagonal bisects the parallelogram into two congruent triangles
The Sum of the square of all the sides of a parallelogram is equal to the sum of the square of its diagonals. It is also called parallelogram law

Also, read:

Parallelogram Law
Diagonal of a Parallelogram Formula
Of import Questions Class 9 Maths Chapter ix Areas Parallelograms

Formulas (Area & Perimeter)

The formula for the area and perimeter of a parallelogram is covered here in this section. Students can use these formulas and solve bug based on them.

Area of Parallelogram

Area of a parallelogram is the region occupied by it in a 2-dimensional airplane. Below is the formula to find the parallelogram area:

Area = Base × Summit

Parallelogram 2

In the in a higher place figure, ||^gramABCD, Surface area is given by;

Surface area = a b sin A = b a sin B

where a is the camber length of the side of ||^gramABCD and b is the base.

Bank check hither: Expanse of a Parallelogram Formula

Perimeter of Parallelogram

The perimeter of any shape is the full altitude covered around the shape or the full length of any shape. Similarly, theperimeter of a parallelogram is the full altitude of the boundaries of the parallelogram. To calculate the perimeter value, nosotros accept to know the values of its length and breadth. The parallelogram has its reverse sides equal in length. Therefore, the formula to calculate the perimeter is written as;

Perimeter = two (a+b) units

Where a and b are the length of the sides of the parallelogram.

Types of Parallelogram

At that place are mainly four types of parallelograms, depending on various factors. The factors which distinguish between all of these different types of parallelogram are angles, sides etc.

In a parallelogram, say PQRS
- If PQ = QR = RS = SP are the equal sides, so information technology's a rhomb. All the backdrop are the same for rhombus as for parallelogram.
Other two special types of a parallelogram are:
- Rectangle
- Foursquare

Is Foursquare a Parallelogram?

Yep, a square is considered every bit a parallelogram since the opposite sides are parallel to each other, and the diagonals of the square bisect each other.

Is Rectangle a Parallelogram?

Yes, a rectangle is also a parallelogram, because information technology satisfies the conditions or meets the backdrop of parallelogram such as the opposite sides are parallel and diagonals bisect each other.

Parallelogram Theorems

Theorem 1:Parallelograms on the same base and between the same parallel sides are equal in area.

Proof: 2 parallelograms ABCD and ABEF, on the aforementioned base DC and between the same parallel line AB and FC.

To bear witness that surface area (ABCD) = surface area (ABEF).

Parallelogram 3

Proof:

Consider the above figure –

In ∆ADF and ∆BCE,

AD = BC (Since, ABCD is a parallelogram ∴ Advertizement=BC)

AF = BE (Since, ABEF is a parallelogram ∴AF=BE)

∠ADF = ∠BCE (Corresponding Angles)

∠AFD = ∠BEC (Corresponding Angles)

∠DAF = ∠CBE (Angle Sum Property)

Therefore, ∆ADE ≅ ∆BCF (From SAS-rule)

Expanse(ADF) = Area(BCE) (By congruence area precept)

Area(ABCD) = Area(ABED) + Area(BCE)

Area(ABCD) = Area(ABED)+Area(ADF)

Surface area(ABCD) = Expanse(ABEF)

Hence, the area of parallelograms on the aforementioned base and between the same parallel sides is equal.

Corollary

A parallelogram and a rectangle on the aforementioned base of operations and between the same parallels are equal in surface area.

Proof: Since a rectangle is besides a parallelogram and so, the outcome is a direct consequence of the above theorem.

Theorem:The area of a parallelogram is the product of its base and the corresponding altitude.

Given: In a parallelogram ABCD, AB is the base.

To prove that Surface area(||^gmABCD) = AB×AL

Structure: Complete the rectangle ALMB by Drawing BM perpendicular to CD.

Parallelogram 4
Consider the effigy given beneath:

Parallelogram ABCD and rectangle ABML are on the same base and betwixt the same parallels AB and LC.

area of parallelogram ABCD = expanse of parallelogram ABML

Nosotros know that expanse of a rectangle = length x breadth.

Therefore, expanse of parallelogram ABCD = AB x AL

Hence, the area of a parallelogram is the product of whatever base of it and the corresponding altitude.

Departure Betwixt Parallelogram and Rhomb

Parallelogram	Rhombus
A quadrilateral that has its reverse sides equal and parallel	A quadrilateral that has all its sides coinciding
Diagonals bisect each other	Diagonals bisect each other at 90 degrees
Contrary angles are of equal measure	All iv angles are of equal measure

Examples on Parallelogram

Example 1:

Find the area of a parallelogram whose base is 5 cm and height is 8 cm.

Solution-:

Given, Base of operations = v cm and Peak = 8 cm.

Nosotros know, Area = Base of operations x Elevation

Area = 5 × 8

Area = 40 Sq.cm

Example 2:

Find the area of a parallelogram having a length of diagonals to be 10 and 22 cm and an intersecting angle to be 65 degrees.

Solution:

We know that the diagonals of a parallelogram bisect each other. Hence, one-half the diagonal length will be 5 and 11 cm.

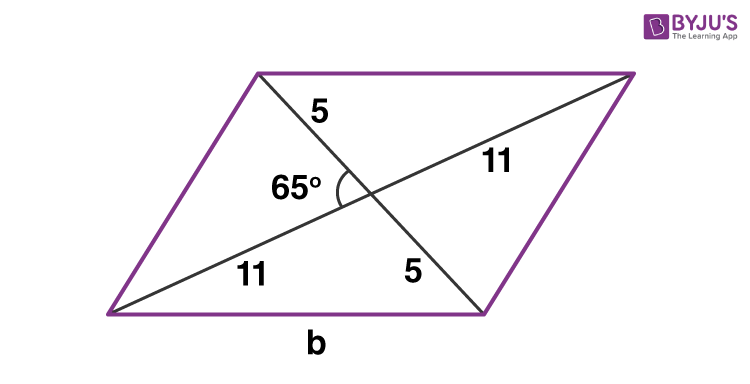
Parallelogram 5

The bending contrary to the side b comes out to be 180 – 65 = 115°

We utilize the constabulary of cosines to calculate the base of the parallelogram –

b² = v² + eleven² – two(11)(five)cos(115°)

b² = 25 + 121 – 110(-0.422)

b² = 192.48

b = thirteen.87 cm.

Parallelogram 6

After finding the base, we need to summate the elevation of the given parallelogram.

To observe the meridian, nosotros have to calculate the value of θ, so we use the sine law

5/sin(θ) = b/sin(115)
θ = 19.06

Parallelogram 7

Now we extend the base of operations and draw in the top of the figure and denote it as 'h'.

The right-angled triangle (marked with a red line) has the Hypotenuse to be 22 cm and the Perpendicular to be h.

Then

sin θ = h/22

h = 7.184 cm

Area = base × height

A = xiii.87 × 7.184

A = 99.645 sq.cm

Hope this word has cleared all your doubts regarding parallelograms and their properties. Annals with BYJU'Due south to learn more than about quadrilaterals and other Maths concepts.

Video Lesson

Frequently Asked Questions (FAQs) on Parallelogram

What is a parallelogram?

A parallelogram is a quadrilateral that has its opposite sides parallel and equal to each other. It has its interior reverse angles equal. As well, the angles on the same side of the transversal sum up to 180 degrees or are supplementary to each other.

What are the examples of a parallelogram?

The parallelogram is quadrilateral which has two pairs of contrary sides parallel and equal. Too, the opposite angles are of equal measure. Examples of shapes that hold the same properties are:
Square
Rectangle
Rhomb
A kit and a trapezium cannot be considered as a parallelogram, as they don't accept two pairs of parallel sides.

What are the area and perimeter of a parallelogram?

The area of a parallelogram is the region occupied past information technology in a two-dimensional plane. Its formula is:
Expanse = Base x Top (in square unit of measurement)
The area of a parallelogram without height is given by:
Expanse = ab sin x
Where a and b are the two adjacent sides of a parallelogram and x is the angle between them.
Perimeter is the total length of boundaries of a parallelogram. It is equal to the sum of all four sides.
Perimeter = two(a+b)

What is the shape of a parallelogram?

A parallelogram is a 4-sided two-dimensional shape with two pairs of sides parallel and equal.

What are the four important properties of a parallelogram?

Opposite sides are parallel and congruent
Reverse angles are congruent
Sequent angles are supplementary
Diagonals bisect each other